Super-recursive algorithm

In computability theory, super-recursive algorithms are a generalization of ordinary algorithms that are more powerful, that is, compute more than Turing machines. The term was introduced by Mark Burgin, whose book "Super-recursive algorithms" develops their theory and presents several mathematical models. Turing machines and other mathematical models of conventional algorithms allow researchers to find properties of recursive algorithms and their computations. In a similar way, mathematical models of super-recursive algorithms, such as inductive Turing machines, allow researchers to find properties of super-recursive algorithms and their computations.

Burgin, as well as other researchers (including Selim Akl, Eugene Eberbach, Peter Kugel, Jan van Leeuwen, Hava Siegelmann, Peter Wegner, and Jiří Wiedermann) who studied different kinds of super-recursive algorithms and contributed to the theory of super-recursive algorithms, have argued that super-recursive algorithms can be used to disprove the Church-Turing thesis, but this point of view has been criticized within the mathematical community and is not widely accepted.

Contents

Definition

Burgin (2005: 13) uses the term recursive algorithms for algorithms that can be implemented on Turing machines, and uses the word algorithm in a more general sense. Then a super-recursive class of algorithms is "a class of algorithms in which it is possible to compute functions not computable by any Turing machine" (Burgin 2005: 107).

Super-recursive algorithms are closely related to hypercomputation in a way similar to the relationship between ordinary computation and ordinary algorithms. Computation is a process, while an algorithm is a finite constructive description of such a process. Thus a super-recursive algorithm defines a "computational process (including processes of input and output) that cannot be realized by recursive algorithms." (Burgin 2005: 108). A more restricted definition demands that hypercomputation solves a supertask (see Copeland 2002; Hagar and Korolev 2007).

Super-recursive algorithms are also related to algorithmic schemes, which are more general than super-recursive algorithms. Burgin argues (2005: 115) that it is necessary to make a clear distinction between super-recursive algorithms and those algorithmic schemes that are not algorithms. Under this distinction, some types of hypercomputation are obtained by super-recursive algorithms, e.g., inductive Turing machines, while other types of hypercomputation are directed by algorithmic schemas, e.g., infinite time Turing machines. This explains how works on super-recursive algorithms are related to hypercomputation and vice versa. According to this argument, super-recursive algorithms are just one way of defining a hypercomputational process.

Examples

Examples of super-recursive algorithms include (Burgin 2005: 132):

Examples of algorithmic schemes include:

For examples of practical super-recursive algorithms, see the book of Burgin.

Inductive Turing machines

Inductive Turing machines implement an important class of super-recursive algorithms. An inductive Turing machine is a definite list of well-defined instructions for completing a task, when given an initial state, will proceed through a well-defined series of successive states, eventually giving the final result. The difference between an inductive Turing machine and an ordinary Turing machine is that an ordinary Turing machine must stop when it has obtained its result, while in some cases an inductive Turing machine can continue to compute after obtaining the result, without stopping. Kleene called procedures that could run forever without stopping by the name calculation procedure or algorithm (Kleene 1952:137). Kleene also demanded that such an algorithm must eventually exhibit "some object" (Kleene 1952:137). Burgin argues that this condition is satisfied by inductive Turing machines, as their results are exhibited after a finite number of steps. The reason that inductive Turing machines cannot be instructed to halt when their final output is produced is that in some cases inductive Turing machines may not be able to tell at which step the result has been obtained.

Simple inductive Turing machines are equivalent to other models of computation such as general Turing machines of Schmidhuber, trial and error predicates of Hilary Putnam, limiting partial recursive functions of Gold, and trial-and-error machines of Hintikka and Mutanen. More advanced inductive Turing machines are much more powerful. There are hierarchies of inductive Turing machines that can decide membership in arbitrary sets of the arithmetical hierarchy (Burgin 2005). In comparison with other equivalent models of computation, simple inductive Turing machines and general Turing machines give direct constructions of computing automata that are thoroughly grounded in physical machines. In contrast, trial-and-error predicates, limiting recursive functions, and limiting partial recursive functions present only syntactic systems of symbols with formal rules for their manipulation. Simple inductive Turing machines and general Turing machines are related to limiting partial recursive functions and trial-and-error predicates as Turing machines are related to partial recursive functions and lambda calculus.

The non-halting computations of inductive Turing machines should not be confused with infinite-time computations (see, for example, Potgieter 2006). First, some computations of inductive Turing machines do halt. As in the case of conventional Turing machines, some halting computations give the result, while others do not. Even it does not halt, an inductive Turing machine produces output from time to time. If this output stops changing, it is then considered the result of the computation.

There are two main distinctions between ordinary Turing machines and simple inductive Turing machines. The first distinction is that even simple inductive Turing machines can do much more than conventional Turing machines. The second distinction is that a conventional Turing machine will always determine (by coming to a final state) when the result is obtained, while a simple inductive Turing machine, in some cases (such as when "computing" something that cannot be computed by an ordinary Turing machine), will not be able to make this determination.

Schmidhuber's generalized Turing machines

A symbol sequence is computable in the limit if there is a finite, possibly non-halting program on a universal Turing machine that incrementally outputs every symbol of the sequence. This includes the dyadic expansion of π but still excludes most of the real numbers, because most cannot be described by a finite program. Traditional Turing machines cannot edit their previous outputs; generalized Turing machines, according to Jürgen Schmidhuber, can. He defines the constructively describable symbol sequences as those that have a finite, non-halting program running on a generalized Turing machine, such that any output symbol eventually converges, that is, it does not change any more after some finite initial time interval. Due to limitations first exhibited by Kurt Gödel (1931), it may be impossible to predict the convergence time itself by a halting program, otherwise the halting problem could be solved. Schmidhuber (2000, 2002) uses this approach to define the set of formally describable or constructively computable universes or constructive theories of everything. Generalized Turing machines and simple inductive Turing machines are two classes of super-recursive algorithms that are the closest to recursive algorithms.

Relation to the Church–Turing thesis

The Church–Turing thesis in recursion theory relies on a particular definition of the term algorithm. Based on definitions that are more general than the one commonly used in recursion theory, Burgin argues that super-recursive algorithms, such as inductive Turing machines disprove the Church–Turing thesis. He proves furthermore that super-recursive algorithms could theoretically provide even greater efficiency gains than using quantum algorithms.

Burgin's interpretation of super-recursive algorithms has encountered opposition in the mathematical community. One critic is logician Martin Davis, who argues that Burgin's claims have been well understood "for decades". Davis states,

"The present criticism is not about the mathematical discussion of these matters but only about the misleading claims regarding physical systems of the present and future."(Davis 2006: 128)

Davis disputes Burgin's claims that sets at level 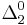\Delta^0_2 of the arithmetical hierarchy can be called computable, saying

"It is generally understood that for a computational result to be useful one must be able to at least recognize that it is indeed the result sought." (Davis 2006: 128)

References

External links